(c) Freepik28 octobre 2025
Il m’arrive par moment de me piquer d’intérêt pour les vidéos de voyage et « d’aventure » sur YouTube (l’aventure pouvant parfois se résumer à une promenade en nature). Un thème récurrent dans les médias de ce genre est le choix d’un point au hasard avec l’objectif de s’y rendre, voire d’en revenir (exemple 1, exemple 2).
L’algorithme de choix n’est généralement pas excessivement détaillé, ou alors se résume en un choix dans un rectangle compris entre deux méridiens et deux parallèles, ce qui n’est pas très enthousiasmant comme problème à résoudre. En effet, il suffit dans un rectangle de choisir une abscisse et une ordonnée entre les deux bornes limites. Mon tropisme naturel et mon esprit franco-centré m’a donc naturellement conduit à me poser la question la plus naturelle : comment ferait-on pour choisir un point au hasard en France ?
Un premier instinct serait de délimiter la France dans un rectangle (ou plusieurs rectangle) et de croiser les doigts pour ne pas tomber dans l’eau ou un pays limitrophe. Ou alors recommencer jusqu’à ce qu’on tombe juste. Mais ce n’est pas très élégant et encore faudrait-il être capable de déterminer algorithmiquement si un point est bien sur le territoire français. Et pour cela, il va nous falloir quelques données.
Je me suis d’abord lancé à la recherche d’une liste des points frontaliers de la France. Je pensais naïvement que je trouverais ça avec l’API d’Etalab geo.api.gouv.fr, qui fournit déjà le tracé des communes, départements et régions, mais en fait non. Je me suis ensuite tourné vers l’IGN, mais chou blanc également. C’est donc sur OpenStreetMap que j’ai fini par trouver mon bonheur, mais ça n’a pas été une sinécure. Alors que je pensais m’en tirer avec un bête clic droit « Télécharger la frontière », c’est sur l’obscur overpass-turbo.eu que j’ai fini par trouver mon bonheur, avec cette requête que je ne saurai plus vous expliquer, probablement tirée de la lecture croisée de trois forums différents.
[out:json][timeout:25]
relation(16467322);
(._;>;);
out body;
J’en ai donc tiré un fichier GeoJSON contenant une liste de près de 2 000 polygones formant la France métropolitaine, les plus grands constituant la France continentale (380 365 côtés), puis la Corse (79 359 côtés) et Ouessant (16 678 côtés). Autant dire qu’on suit le tracé de la frontière d’assez près.
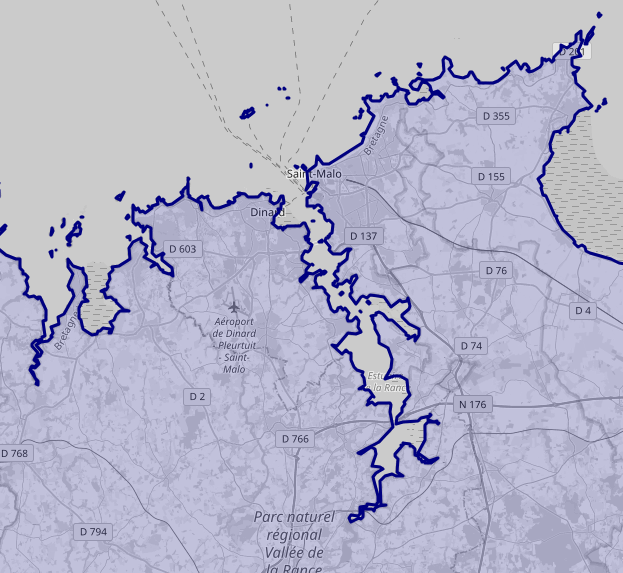Paradoxe du littoral, illustration.
Maintenant qu’on a ces informations, la réflexion peut commencer. Le prochain défi est de passer de la représentation géographique à la représentation géométrique. Tous ces points doivent être placés sur une carte. Pour cela, le choix d’une méthode de projection s’impose. Après quelques recherches, la projection conique conforme de Lambert paraît être le système de référence en France métropolitaine (il y a même un décret dessus, c’est dire si c’est sérieux). Son principal défaut cependant est d’être parfaitement imbuvable et d’une complexité bien supérieure à l’ambition initiale du projet et à mes propres compétences en la matière.
J’ai donc opté pour une méthode plus simple à mettre en œuvre, en l’espèce la projection sinusoïdale : l’ordonnée d’un point est proportionnelle à sa latitude, et l’abscisse est ajustée proportionnellement à la longitude et au cosinus de la latitude (si vous me permettez un excès d’arrogance, j’ai redécouvert la méthode par moi-même avant de découvrir qu’elle avait déjà un nom). L’enjeu est d’assurer une représentation à peu près réaliste des surfaces. Sinon, en assimilant longitude et latitude à abscisse et ordonnée comme dans la projection de Mercator, on représente le nord de façon disproportionnée par rapport au sud et le tirage aléatoire d’un point n’est plus uniforme sur le territoire. Dans le détail, on pose les variables suivantes :
Puis on définit pour notre convenance la variable \(r\) suivante :
On peut enfin faire nos calculs, avec \(x\) le numéro de colonne du pixel correspondant au point sur l’image et \(y\) le numéro de ligne :
$$x = M+\frac{L}{2}+r\cdot\left(\lambda-\frac{\lambda_{max}-\lambda_{min}}{2}\right) \cdot \cos \left(\phi\right)$$
$$y = M+r\cdot\left(\phi_{max}-\phi\right)$$
Après des calculs dûment réalisés on obtient la représentation suivante, ma foi pas honteuse :
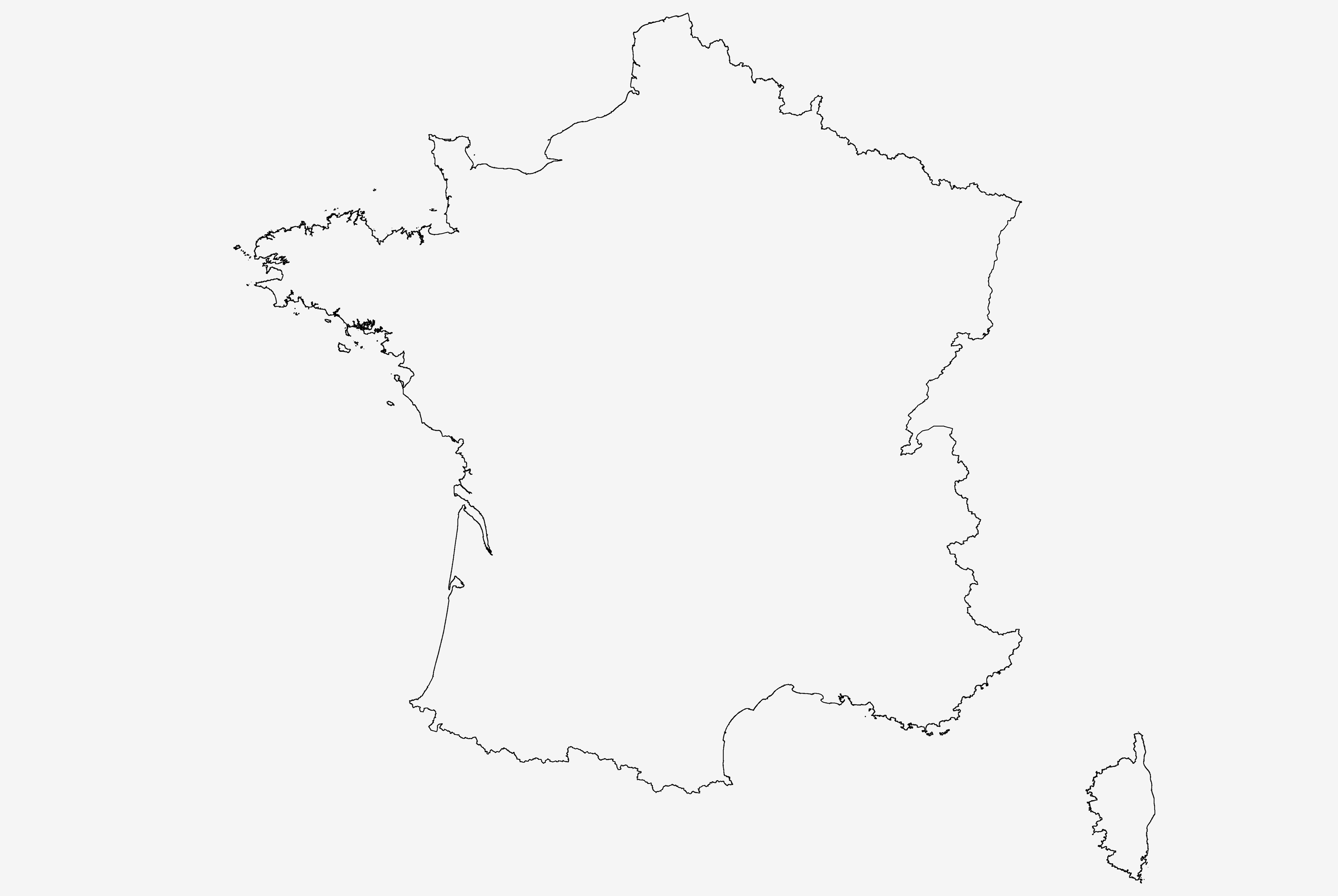Hum, oui, c’est la France quoi
Une note : pour placer les points sur l’image on prend des valeurs entières de \(x\) et \(y\), mais pour la précision des calculs on conserve les valeurs flottantes (avec des chiffres après la virgule).
L’enjeu à présent est de réussir à choisir un point au hasard dans un de nos polygones de façon uniforme. Pour cela on ne va pas utiliser la méthode évoquée plus haut du point tiré dans un rectangle jusqu’à tomber sur le territoire. On va partir sur un autre procédé plus satisfaisant (à mon sens, vous savez, les goûts et les couleurs). En l’espèce, les polygones ont le bon goût de tous pouvoir être découpés en triangles et l’algorithme pour choisir un point au hasard dans un triangle est simple à mettre en œuvre. Prochaine étape donc : la triangulation du territoire (hommage aux Cassini). Pour cela, j’ai repris le code de ce dépôt sur GitHub, qui a bien fait le travail.
Enfin bon, il a bien fait le travail mais il a quand même pris son temps, le bougre. 30 heures. Je veux bien croire que mon PC n’est pas une bête de course mais soyons sérieux.
Deux dodos plus tard, donc, j’avais à disposition une liste d’environ 600 000 triangles (pour à peu près autant de points dans mon fichier d’origine). Le plus petit est de l’ordre de \(10^{-15}\) pixels (vous n’aviez sûrement encore jamais vu de femto-pixels auparavant) du côté de l’Île d’Yeu ; le plus grand est de l’ordre de 1,3 million de pixels ; et la surface totale couverte est d’environ 5,1 millions de pixels. Pour le plaisir de vos yeux voici à quoi ressemble la triangulation sur la carte.
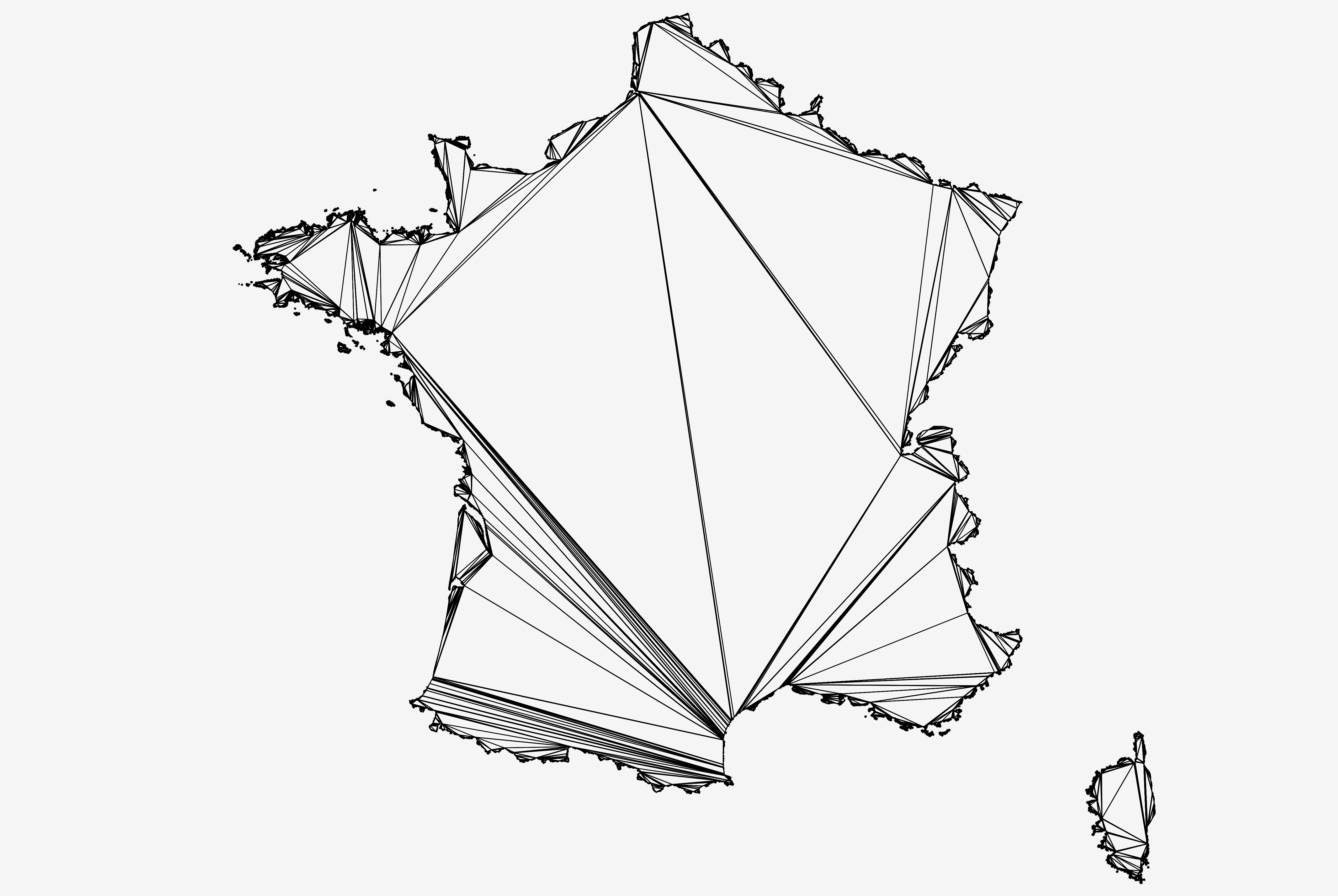La France est divisée.
Le calcul de l’aire de chaque triangle permet de choisir un triangle au hasard en pondérant selon la surface : il faut en effet qu’on ait un peu plus de chance de tomber sur notre gros triangle qui occupe un quart de la surface du pays que sur notre micro-machin dans l’Atlantique. Notez que je parle ici de surfaces mesurées en pixels mais l’idée est d’avoir des valeurs proportionnelles aux vraies aires. Les superficies inférieures à un pixel sont théoriques, d’une part car invisibles sur la carte, et d’autre part leur probabilité d’être choisie est négligeable. Je les ai tout de même inclues dans mes petits calculs par soucis de complétude.
Pour choisir un triangle au hasard, on classe nos triangles par ordre de taille, du plus petit au plus grand, et on crée à côté une liste des surfaces cumulées de nos triangles : la première valeur est égale à la surface du premier triangle, la deuxième à la somme des surfaces des deux premiers triangles, la troisième des trois premiers… puis la dernière valeur de la liste est la surface totale des triangles. Il ne nous reste plus qu’à choisir un nombre au hasard entre 0 et la surface totale, et on remonte la liste des surfaces cumulées jusqu’à dépasser la valeur tirée. Notre position dans la liste indique le triangle retenu.
Pour choisir un point au hasard dans le triangle, j’ai adapté la méthode proposée ici sur Stackoverflow par un aimable contributeur.
Pour la mise en œuvre pratique de ces considérations algorithmiques, j’ai fini par mettre de côté Python. En effet, les scripts dans le terminal, c’est rigolo mais ce n’est pas très visuel et c’est difficile d’accès. J’ai donc entrepris le développement d’une page web dédiée pour la démonstration (eh oui, vous pourrez jouer à la fin de l’article, tout ceci n’est pas purement théorique). L’objectif est d’avoir un gros bouton qui affiche un point sur la carte et les coordonnées géographiques correspondantes.
En synthèse, j’affiche sur la page ma carte que je vous ai montré au début et je superpose par dessus un objet <canvas>. Quand je clique sur un bouton, les opérations que je vous ai décrites juste avant se réalisent : choix d’un triangle et choix d’un point dans le triangle. Il n’y a plus qu’à faire les opérations pour la projection que je vous ai décrites précédemment en sens inverse. Pour placer le point sur la carte, il faut prendre en compte le redimensionnement de l’image mais rien de plus compliqué qu’une règle de trois.
Je vous passerai mes prises de tête avec Javascript et le CSS pour que tout soit aligné comme il faut, mais j’ai tout de même rencontré un petit souci pratique qui vaut bien un détour : la liste des triangles occupe relativement beaucoup de place (75 Mo) et la page prend bien dix secondes à se charger (sur mon ordinateur encore une fois, ce n’est pas une référence absolue mais ça incite à se poser des questions d’optimisation). Plutôt que de charger les triangles avec une balise <script> j’ai donc opté pour une solution alternative où tous mes triangles sont répartis dans autant de fichiers (près de 600 000 donc). Une fois que je connais l’index du triangle dans lequel je vais faire la suite de mes opérations, je l’appelle unitairement dynamiquement (les fichiers s’appellent 0, 1, 2... 599591 et font quelques octets chacun) pour un « coût » minime (si ce n’est l’enfer de gérer de l’asynchrone et les promesses Javascript).
Le site est statique et fonctionne complètement en local. Si vous voulez récupérer le code, vous pouvez faire Ctrl+U. Il faudra aussi penser à récupérer tout le contenu du dossier script/triangles/.
Évidemment, alors que j’écris ces lignes, j’ai entamé la copie des fichiers vers le serveur et je commence à remettre en question la pertinence de mes choix parce que 600 000 fichiers de 100 octets prennent bien plus de temps à la copie qu’un seul faisant la même taille cumulée. Tous ces femto-pixels valaient-ils vraiment la peine d’être pris en considération ?
Trève de plaisanterie, vous pouvez vous amuser dès maintenant en cliquant juste en dessous.
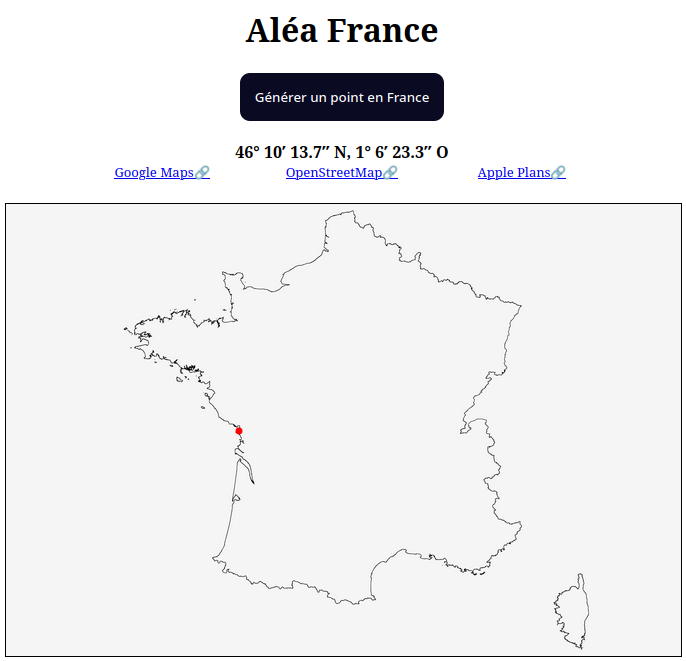Je ne suis toujours pas web designer.
J’ai hésité à finasser avec des fonctionnalités supplémentaires, pour pouvoir choisir le territoire sur lequel on veut tirer notre point au hasard (commune, département, région, outre-mer compris), un historique des points tirés avec possibilité de conserver les points sur la carte au fur et à mesure, un cookie pour retrouver son historique quand on retourne sur la page, un appel API pour afficher la commune d’atterrissage… Bref, les idées ne manquaient pas, mais il faut aussi savoir se satisfaire d’un produit qui fonctionne. Je laisse quand même cette road map ici si la motivation me revient.
Pour ce qui me concerne, je ne suis pas encore parti à l’aventure. Ça viendra peut-être. J’avoue que je me suis lancé tête baissée dans le développement de ce machin en étant plus séduit par l’exercice intellectuelle que par un besoin réelle. Mais maintenant que c’est fait, charge à vous de vous en saisir, moi j’ai fait ma part du travail.
Merci pour votre attention.